Grupo (matemáticas)

Un grupo es una estructura algebraica formada por un conjunto no vacío y una operación que cumple las siguientes:

1. La operación, por ejemplo ⋆, combina cualquier par de elementos para componer un tercero dentro del mismo conjunto;
2. Satisface la propiedad asociativa, de existencia del elemento neutro o identidad, x, para todo y del grupo, x⋆y = y⋆x = y, y de existencia de elementos inversos, z, para todo y del grupo, z⋆y=y⋆z=x.

Si es conmutativo siempre, es conjunto abeliano.

Un subgrupo es aquel que tiene como conjunto un subconjunto del grupo original, y la misma operación. Por ejemplo, el subgrupo normal.

Grupo simétrico

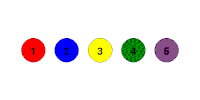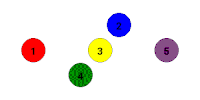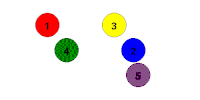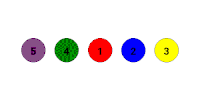
La colección de posibles permutaciones (reordenamientos) de un conjunto de algunos elementos es un grupo. Un par de permutaciones bajo la operación se envía a otra permutación.

El grupo simétrico es aquel cuyos elementos son un número de elementos que se reordenan, y cada posible ordenamiento es un elemento diferente.

El conjunto de las operaciones bajo una operación que se define entre dos permutaciones forma un grupo.

Referencias