Statistics/Distributions/Exponential

Exponential
	Probability density function;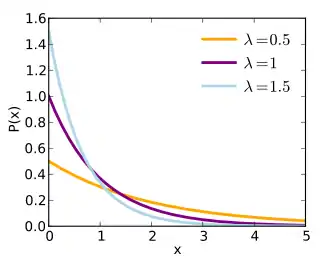
	Cumulative distribution function;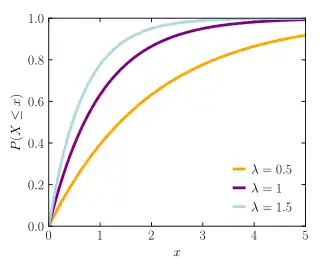
Parameters	λ > 0 rate, or inverse scale
Support	x ∈ [0, ∞)
PDF	λ e−λx
CDF	1 − e−λx
Mean	λ−1
Median	λ−1 ln 2
Mode	0
Variance	λ−2
Skewness	2
Ex. kurtosis	6
Entropy	1 − ln(λ)
MGF
CF

Exponential Distribution

Exponential distribution refers to a statistical distribution used to model the time between independent events that happen at a constant average rate λ. Some examples of this distribution are:

The distance between one car passing by after the previous one.
The rate at which radioactive particles decay.

For the stochastic variable X, probability distribution function of it is:

$f_{x}(x)={\begin{cases}\lambda e^{-\lambda x},&{\mbox{if }}x\geq 0\\0,&{\mbox{if }}x<0\end{cases}}$

and the cumulative distribution function is:

$F_{x}(x)={\begin{cases}0,&{\mbox{if }}x<0\\{1-e^{-\lambda x}},&{\mbox{if }}x\geq 0\end{cases}}$

Exponential distribution is denoted as $X\in {\mbox{Exp(m)}}$ , where m is the average number of events within a given time period. So if m=3 per minute, i.e. there are three events per minute, then λ=1/3, i.e. one event is expected on average to take place every 20 seconds.

Mean

We derive the mean as follows.

\operatorname {E} [X]=\int _{-\infty }^{\infty }x\cdot f(x)dx

\operatorname {E} [X]=\int _{0}^{\infty }x\lambda e^{-\lambda x}dx

\operatorname {E} [X]=\int _{0}^{\infty }(-x)(-\lambda e^{-\lambda x})dx

We will use integration by parts with u=−x and v=e^−λx. We see that du=-1 and dv=−λe^−λx.

\operatorname {E} [X]=\left[-x\cdot e^{-\lambda x}\right]_{0}^{\infty }-\int _{0}^{\infty }(e^{-\lambda x})(-1)dx

\operatorname {E} [X]=[0-0]+\left[{-1 \over \lambda }(e^{-\lambda x})\right]_{0}^{\infty }

\operatorname {E} [X]=\left[0-{-1 \over \lambda }\right]

\operatorname {E} [X]={1 \over \lambda }

Variance

We use the following formula for the variance.

\operatorname {Var} (X)=\operatorname {E} [X^{2}]-(\operatorname {E} [X])^{2}

\operatorname {Var} (X)=\int _{-\infty }^{\infty }x^{2}\cdot f(x)dx-\left({2}\right)^{2}

\operatorname {Var} (X)=\int _{0}^{\infty }x^{2}e^{-2x}dx-{2}

We'll use integration by parts with $u=-x^{2}$ and $v=e^{-2x}$ . From this we have $du=-2x$ and $v=-2e^{-2x}$ .

\operatorname {Var} (X)=\left\{\left[-x^{2}\cdot e^{-\lambda x}\right]_{0}^{\infty }-\int _{0}^{\infty }(e^{-\lambda x})(-2x)dx\right\}-{1 \over \lambda ^{2}}

\operatorname {Var} (X)=[0-0]+{2 \over \lambda }\int _{0}^{\infty }x\lambda e^{-\lambda x}dx-{1 \over \lambda ^{2}}

We see that the integral is just $\operatorname {E} [X]$ which we solved for above.

\operatorname {Var} (X)={2 \over \lambda }{1 \over \lambda }-{1 \over \lambda ^{2}}

\operatorname {Var} (X)={1 \over \lambda ^{2}}

External links

Interactive Exponential Distribution Web Applet (Java)

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.