Statistics/Distributions/Uniform

Uniform
	Probability density function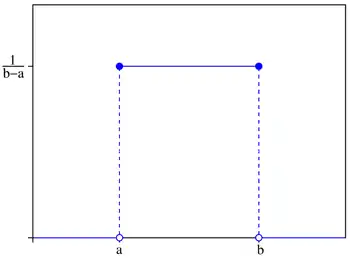; ; Using maximum convention
	Cumulative distribution function;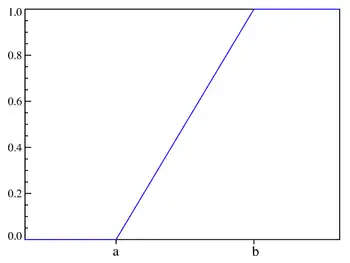
Notation
Parameters
Support
PDF
CDF
Mean
Median
Mode	any value in
Variance
Skewness	0
Ex. kurtosis
Entropy
MGF
CF

Continuous Uniform Distribution

The (continuous) uniform distribution, as its name suggests, is a distribution with probability densities that are the same at each point in an interval. In casual terms, the uniform distribution shapes like a rectangle.

Mathematically speaking, the probability density function of the uniform distribution is defined as

$f\colon [a,b]\to \mathbb {R}$

$f\left(x\right)={1 \over {b-a}}$

And the cumulative distribution function is:

$F\left(x\right)={\begin{cases}0,&{\mbox{if }}x\leq a\\{{x-a} \over {b-a}},&{\mbox{if }}a<x<b\\1,&{\mbox{if }}x\geq b\end{cases}}$

Mean

We derive the mean as follows.

\operatorname {E} [X]=\int _{-\infty }^{\infty }xf(x)dx

As the uniform distribution is 0 everywhere but [a, b] we can restrict ourselves that interval

\operatorname {E} [X]=\int _{a}^{b}{1 \over {b-a}}xdx

\operatorname {E} [X]=\left.{1 \over (b-a)}{1 \over 2}x^{2}\right|_{a}^{b}

\operatorname {E} [X]={1 \over 2(b-a)}\left[b^{2}-a^{2}\right]

\operatorname {E} [X]={b+a \over 2}

Variance

We use the following formula for the variance.

\operatorname {Var} (X)=\operatorname {E} [X^{2}]-(\operatorname {E} [X])^{2}

\operatorname {Var} (X)=\left[\int _{-\infty }^{\infty }f(x)\cdot x^{2}dx\right]-\left({b+a \over 2}\right)^{2}

\operatorname {Var} (X)=\left[\int _{a}^{b}{1 \over {b-a}}x^{2}dx\right]-{(b+a)^{2} \over 4}

\operatorname {Var} (X)=\left.{1 \over {b-a}}{1 \over 3}x^{3}\right|_{a}^{b}-{(b+a)^{2} \over 4}

\operatorname {Var} (X)={1 \over 3(b-a)}[b^{3}-a^{3}]-{(b+a)^{2} \over 4}

\operatorname {Var} (X)={4(b^{3}-a^{3})-3(b+a)^{2}(b-a) \over 12(b-a)}

\operatorname {Var} (X)={(b-a)^{3} \over 12(b-a)}

\operatorname {Var} (X)={(b-a)^{2} \over 12}

External links

Interactive Uniform Distribution Web Applet (Java)

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

Uniform
Probability density function Using maximum convention
Cumulative distribution function
Notation	${\mathcal {U}}(a,b)$
Parameters	$-\infty <a<b<\infty \,$
Support	$x\in [a,b]$
PDF	${\begin{cases}{\frac {1}{b-a}}&{\text{for }}x\in [a,b]\\0&{\text{otherwise}}\end{cases}}$
CDF	${\begin{cases}0&{\text{for }}x<a\\{\frac {x-a}{b-a}}&{\text{for }}x\in [a,b)\\1&{\text{for }}x\geq b\end{cases}}$
Mean	${\tfrac {1}{2}}(a+b)$
Median	${\tfrac {1}{2}}(a+b)$
Mode	any value in $[a,b]$
Variance	${\tfrac {1}{12}}(b-a)^{2}$
Skewness	0
Ex. kurtosis	$-{\tfrac {6}{5}}$
Entropy	$\ln(b-a)\,$
MGF	${\frac {\mathrm {e} ^{tb}-\mathrm {e} ^{ta}}{t(b-a)}}$
CF	${\frac {\mathrm {e} ^{itb}-\mathrm {e} ^{ita}}{it(b-a)}}$