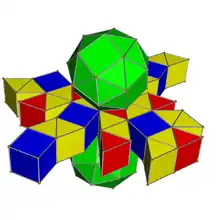
| Snub cubic prism | |
|---|---|
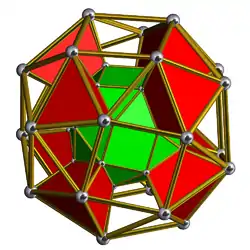 Schlegel diagram | |
| Type | Prismatic uniform polychoron |
| Uniform index | 56 |
| Schläfli symbol | sr{4,3}×{} |
| Coxeter-Dynkin | |
| Cells | 40 total: |
| Faces | 136 total: 64 {3} 72 {4} |
| Edges | 144 |
| Vertices | 48 |
| Vertex figure | 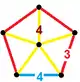 irr. pentagonal pyramid |
| Symmetry group | [(4,3)+,2], order 48 |
| Properties | convex |
In geometry, a snub cubic prism or snub cuboctahedral prism is a convex uniform polychoron (four-dimensional polytope).
It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.
See also
- Snub cubic antiprism s{4,3,2} - A related nonuniform polychoron
Alternative names
- Snub-cuboctahedral dyadic prism (Norman W. Johnson)
- Sniccup (Jonathan Bowers: for snub-cubic prism)
- Snub-cuboctahedral hyperprism
- Snub-cubic hyperprism
External links
- 6. Convex uniform prismatic polychora - Model 56, George Olshevsky.
- Klitzing, Richard. "4D uniform polytopes (polychora) s3s4s x - sniccup".
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.