Base canónica

Every vector a in three dimensions is a linear combination of the standard basis vectors i, j and k.

La base canónica de un espacio vectorial bajo un cuerpo como los números reales con una dimensión n menor que infinito, es decir, finitamente generado, es aquel conjunto de vectores cuya única coordenada distinta de cero vale 1, hay n vectores, y cada uno de los n vectores ordenados como v1, v2, v3, …, vn, donde 1, 2, 3, …, n es el subíndice, tiene como coordenada 1 la que ocupa la posición que indica el subíndice.

Así, la base canónica de un cuerpo de dimensión 2 puede entenderse como un eje de coordenadas donde uno de los ejes representa la primera coordenada, y el otro eje representa la segunda coordenada.

A veces, es fácil entender que son aquellos vectores con coordenadas ceros excepto una que es 1, ya que la base canónica de las matrices 2x2 es:

${\displaystyle \mathbf {e} _{11}={\begin{pmatrix}1&0\\0&0\end{pmatrix}},\quad \mathbf {e} _{12}={\begin{pmatrix}0&1\\0&0\end{pmatrix}},\quad \mathbf {e} _{21}={\begin{pmatrix}0&0\\1&0\end{pmatrix}},\quad \mathbf {e} _{22}={\begin{pmatrix}0&0\\0&1\end{pmatrix}}.}$

Como en cualquier base, el orden es importante y cualquier reordenamiento (permutación) de esta base no resulta ser la base canónica.

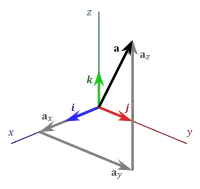
Con la base canónica del cuerpo de los números reales, R, de dimensión 3, R^3, C3 = ((1, 0, 0), (0, 1, 0), (0, 0, 1)) se puede escribir como combinación lineal de estos vectores. Por ejemplo, el vector (a, b, c) = a*(1, 0, 0) + b*(0, 1, 0) + c*(0, 0, 1).

Por el lema de Steinitz, cualquier combinación lineal por cambios elementales al colocar la base canónica en columnas (en caso de matrices en orden de izquierda a derecha, de arriba a abajo en la matriz para que quede cuadrada), es una base del espacio vectorial.

Referencias