In knot theory, a prime knot or prime link is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-trivial knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite knots or composite links. It can be a nontrivial problem to determine whether a given knot is prime or not.
A family of examples of prime knots are the torus knots. These are formed by wrapping a circle around a torus p times in one direction and q times in the other, where p and q are coprime integers.
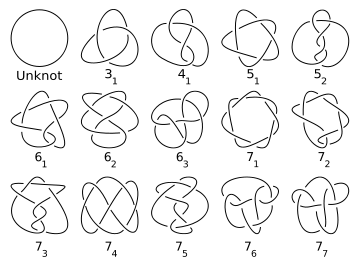
Knots are characterized by their crossing numbers. The simplest prime knot is the trefoil with three crossings. The trefoil is actually a (2, 3)-torus knot. The figure-eight knot, with four crossings, is the simplest non-torus knot. For any positive integer n, there are a finite number of prime knots with n crossings. The first few values (sequence A002863 in the OEIS) are given in the following table.
n 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Number of prime knots
with n crossings0 0 1 1 2 3 7 21 49 165 552 2176 9988 46972 253293 1388705 Composite knots 0 0 0 0 0 2 1 4 ... ... ... ... Total 0 0 1 1 2 5 8 25 ... ... ... ...
Enantiomorphs are counted only once in this table and the following chart (i.e. a knot and its mirror image are considered equivalent).
Schubert's theorem
A theorem due to Horst Schubert (1919-2001) states that every knot can be uniquely expressed as a connected sum of prime knots.[1]
See also
References
- ↑ Schubert, H. "Die eindeutige Zerlegbarkeit eines Knotens in Primknoten". S.-B Heidelberger Akad. Wiss. Math.-Nat. Kl. 1949 (1949), 57–104.
